딥러닝

인공신경망
- 인간 두뇌의 신경 연결을 흉내 내 데이터에 대한 학습으로 
- 학습 결과가 신경망 내의 내부 가중치로 정해져 결과의 이유를 알기가 어려움 (black boxes)

퍼셉트론
- 여러 개의 입력을 받아 하나의 출력으로 만드는 모델
- 각 입력 값에 해당 가중치를 곱함

계층
뉴런이 모여 하나의 계층을 형성
입력층 -> 은닉층 -> 출력층

모듈
여러 계층(은닉층)이 모여서 특정 덩어리를 만들 수 있음

모델
여러 모듈을 조합해 최종적으로 만드는 신경망

 

선형 vs 비선형

• 선형 (Linear)
  • 데이터의 패턴을 찾고 직선으로 나타낼 수 있음
  • 입력 차원 × 출력 차원 => 가중치 크기

import torch
import torch.nn as nn

# 선형 회귀모델
class LinearRegressionModel(nn.Module):
	# nn.Module의 생성자 메서드 호출
    def __init__(self, input_dim, output_dim):
        super().__init__()		# super() 부모 클래스에 특정 함수 호출
        self.linear = nn.Linear(input_dim, output_dim)

    # 데이터가 정상적으로 입력이 됐다면, 어떻게 동작하는지 정의하는함수
    def forward(self, x):
        return self.linear

 

x = torch.tensor([[1.0, 2.0, 3.0, 4.0]])
model = LinearRegressionModel(input_dim=4, output_dim=6)
output = model(x)

# 모델이 가중치(w)와 편향(b)을 사용해 예측값을 생성
print(output)
# 결과
# tensor([[ 1.5462,  0.5893,  1.4463,  0.5409, -2.9332,  1.1017]],
#       grad_fn=<AddmmBackward0>)

 

super()함수

• 부모 클래스의 메소드를 자식 클래스에서 호출할 때 사용
• 신경망 모델을 만들 때, nn.Module을 상속받을 때 super()를 사용해서 부모 클래스 초기화
• 부모 클래스의 생성자가 먼저 실행된 후 자식 클래스의 생성자 실행

class Parent:
    def __init__(self):
        print("Parent 클래스 생성자 호출")

class Child(Parent):
    def __init__(self):
        super().__init__()  # 부모 클래스의 __init__() 호출
        print("Child 클래스 생성자 호출")

c = Child()
# 결과
# Parent 클래스 생성자 호출
# Child 클래스 생성자 호출

 

• 비선형 (Non-Linear)
  • 단순한 직선으로 데이터를 표현할 수 없음
  • 계층과 비선형 활성화 함수(ReLU, Sigmoid, Tanh)를 사용해 복잡한 관계 학습
    • 여러 은닉층을 쌓아 비선형성 추가
    • 비선형 활성화 함수가 없으면 단순한 선형 모델과 동일해져서 깊은 신경망을 사용할 이유가 없음

 

활성화 함수

• Activation Function
• 입력값을 비선형 변환하여 신경망이 복잡한 패턴을 학습할 수 있도록 하는 함수
• 출력을 결정하는 함수
• 🗃️Sigmoid(입력값을 0~1 사이로 변환), ReLU(음수는 0, 양수는 그대로 출력), Tanh(출력을 -1~1 사이로 변환)

 

딥러닝 학습

최선의 가중치를 결정하는 과정

• 훈련 데이터를 이용해 신경망의 출력이 훈련 데이터의 샘플과 비슷해지는 가중치를 계산
• 동작 4 단계
  • 순전파 -> 손실 계산 -> 역전파 -> 가중치 업데이트
    
    • 순전파 (Forward Propagation): 입력 데이터를 각 계층을 거치면서 계산(가중치 곱하고 편향 더하기), 최종 출력 생성
    • 손실 계산: 실제 값과 예측 값의 차이를 계산하는 과정
    • 역전파: 손실을 줄이기 위해 가중치의 영향력을 계산하는 과정
    • 가중치 업데이트: 최적의 가중치 찾는 과정

 

경사하강법🗃️

정답과 예측 값의 차이가 적어질 수 있게 최적의 가중치 값 찾기

• Gradient Descent
• 손실 함수 (loss function): 실제 값과 예측 값의 차이를 수치로 표현
• 경사 (gradient): 손실 함수의 기울기(변화율)
• 동작
  • 임의의 가중치 부여, 현재 가중치의 gradient 구하기
  • 기울기의 반대 방향으로 가중치 조정 (학습률 α를 곱해서 조절)
  • 이 과정들을 반복하며 손실 값 줄이기 (= 최적의 가중치 찾기)
• 공식
  • w: 가중치, α: 학습률 (한 번에 가중치를 조정하는 크기/ 이동거리 조정값), 기울기: 손실함수 L을 가중치 w에 대해 미분한 값

• "기울기의 반대 방향으로 가야 최솟값으로 간다"
  • 기울기(미분 계수)는 극소값에 가까울 수록 값이 작아짐
  • 기울기가 음수일 때, x의 값이 커질수록 y의 값은 작아지고
  • 기울기가 양수일 때, x의 값이 작아질수록 y의 값이 커짐
  • 이를 이용해 최적의 값을 찾음

 

Q. 경사하강법으로 최적의 기울기를 어떻게 찾나요? +) 왜 미분을 알아야하냐? 🗃️ 편미분을 사용해 손실 함수의 기울기를 계산 -> 극소점(경사가 0이 되는 지점) 찾기 💥 최소 값이 진짜 최소 값이 아닐 수 있음!!

• 미분을 이용한 학습에는 국소 최적값으로 수렴할 문제가 있음
  • 전역 최소값(global minimun)이 아닌 국소 최소값(local minimun)일 수 있다는 의미
  • 신경망이 훈련 데이터에 대해 좋은 결과를 내어 가중치 조정이 더 이상 성능을 향상시키지 않을 경우 최적의 기울기(local minimun)를 찾았다고 판단함
  • 하지만 더 좋은 결과가 나올 수 있는 가중치(global minimun)가 있을 수 있음

 

역전파🗃️

손실을 줄이기 위해 각 가중치가 얼마나 영향을 미쳤는지 계산하는 과정

• Backpropagation
• 과정
  • 출력층에서 입력층 방향으로 손실의 기울기(오차) 계산
  • 오차를 최소화하도록 경사 하강법(미분)을 사용하여 가중치 업데이트
• loss.backward()를 이용해 자동으로 역전파 계산
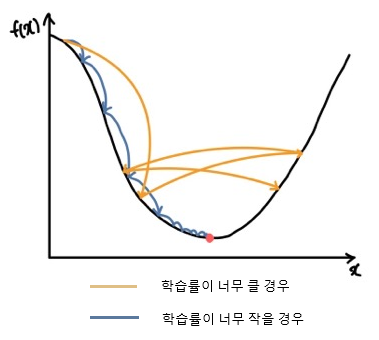
• 학습률 (α)
  • 가중치를 얼마나 이동할 것인지 정하는 파라미터
  • 처음에는 크게 시작, 갈수록 서서히 낮춤
  • 너무 큰 학습률은 최소점에 도달하지 못하고 좌우로 왔다갔다
  • 너무 작은 학습률은 최소점에 느리게 도달